Integração numérica em arquitetura naval - parte 2
A regra de simpson
Na figura a seguir, uma curva passa pelos pontos BCD. Repersenta a integral de f(x). Para calcular a integral de f(x), entre x=A e x=E, vamos aproximar a função por uma parábola que a equação possui a forma: a0+a1x+a2x².
A parábola é representada pela linha pontilhada e corrida. Precisamos de 3 pontos pra definir a curva, então, vamos avaliar os valores de f(x) nos pontos das extremidades e também em um ponto na metade do intervalo, obtendo o ponto C.
AB = f(x1) FC =f(x2) ED = f(x3)
h = AE/2 = (x3-x1)/2
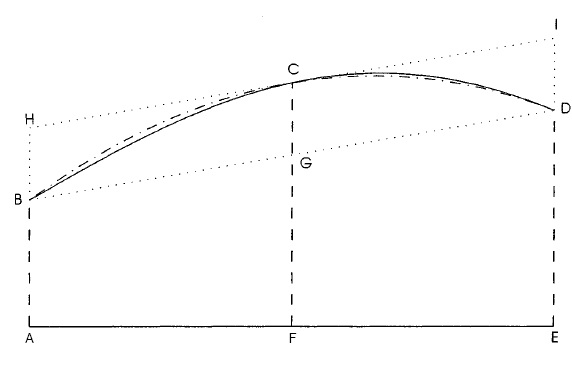
A primeira área é igual a AE x (AB+ED)/2 = 2h x [f(x1) + f(x3)]/2
Para a segunda área, utilizamos uma definição da geometria, que define:"A área de um segmento parabólico é igual a dois terços da área do paralelogramo circunscrito".
Assim, calculamos a segunda área como dois terços do paralelogramo circunscrito BHID:
2/3 x AE x CG = 2/3 x 2h[ f(x2) - f(x1)/2 + f(x3)/2]
Adicionando as duas somas parciais, obtemos:
h/3 [f(x1) +4f(x2) + f(x3)]
Esta é a forma elementar da regra de simpson. Aplicando esta equação para cada par de subintervalos, e adicionando todas as somas parciais, temos:
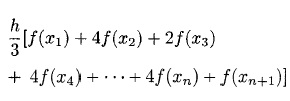
Esta é a fórmula geral da regra de simpson. Utilizando esta mesma fórmula, vamos calcular a mesma integral do exercício do método trapezoidal.
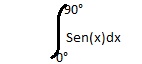
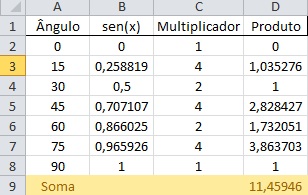
Para obter a aproximação da integral, multiplicamos o valor da soma na coluna pelo intervalo h constante, no caso 15 graus, transformando para radianos:
(15pi/180) x 11,45946/3 = 1,000026
Para um número igual de subintervalos, a regra de simpson produz resultados melhores que a regra trapezoidal.
Segunda regra de simpson
A segunda regra (ou regra dos três oitavos) foi derivada de uma interpolação cúbica, e o número de intervalos deve ser múltiplo de 3. Segue a fórmula geral:
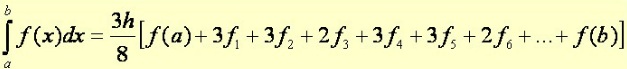
Resolvendo a integral anterior por este método:
| Ângulo | sen(x) | Multiplicador | Produto |
| 0 | 0 | 1 | 0 |
| 15 | 0,258819 | 3 | 0,776457 |
| 30 | 0,5 | 3 | 1,5 |
| 45 | 0,707107 | 2 | 1,414214 |
| 60 | 0,866025 | 3 | 2,598076 |
| 75 | 0,965926 | 3 | 2,897777 |
| 90 | 1 | 1 | 1 |
| Soma | 10,18652 |
Multiplicando o resultado da soma pelo intervalo: (15pi/180) x (3 x 10,18652)/8
temos 1,00006
